概述
java中的indexOf(),Python中的find()函数,底层依赖的就是字符串匹配算法。
字符串匹匹配算法有BF算法,RK算法,BM算法,KMP算法。
其中BF算法RK算法是单模式匹配算法,即为一个串和另一个串进行匹配。
BF算法
Brute Force,即为暴力匹配算法,比较简单,性能不高。
主串的长度记作n,模式串的长度记作m。因为是在主串中查找模式串,所以n>m。在主串中,检查起始位置分别是0、1、…n-m且长度为m的n-m+1个子串,看有没有跟模式串匹配的。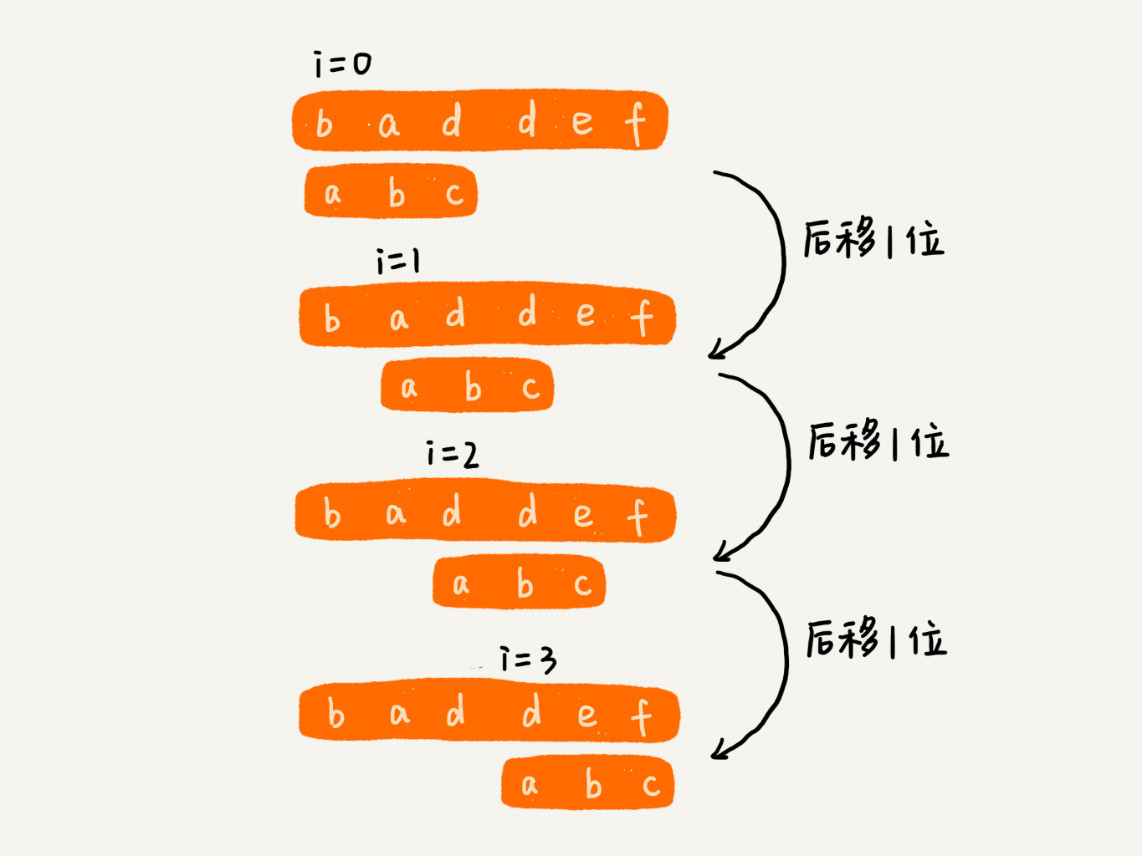
算法最坏时间复杂度为O(n * m)
尽管理论上,BF算法的时间复杂度很高,但在实际的开发中,它却是一个比较常用的字符串匹配算法。
第一,实际的软件开发中,大部分情况下,模式串和主串的长度都不会太长。而且每次模式串与主串中的子串匹配的时候,当中途遇到不能匹配的字符的时候,就可以就停止了,不需要把m个字符都比对一下。所以,尽管理论上的最坏情况时间复杂度是O(n * m),但是,统计意义上,大部分情况下,算法执行效率要比这个高很多。
第二,朴素字符串匹配算法思想简单,代码实现也非常简单。简单意味着不容易出错,如果有bug也容易暴露和修复。在工程中,在满足性能要求的前提下,简单是首选。这也是常说的KISS (Keep it Simple and Stupid)设计原则。
在实际的软件开发中,绝大部分情况下,朴素的字符串匹配算法就够用了。
RK算法
RK算法即为BF算法的升级版。
RK算法的思路为:通过哈希算法对主串中的n-m+1个子串分别求哈希值,然后逐个与模式串的哈希值比较大小。如果某个子串的哈希值与模式串相等,那就说明对应的子串和模式串匹配了。因为哈希值是一个数字,数字之间比较是否相等非常快速的,所以模式串和子串比较的效率就提高了。
为了避免遍历字串中的每一个字符,提高算法的效率,需要对哈希算法进行设计。
假设要匹配的字符串的字符集中只包含K个字符,可以用一个K进制数来表示一个子串,这个K进制数转化成十进制数,作为子串的哈希值。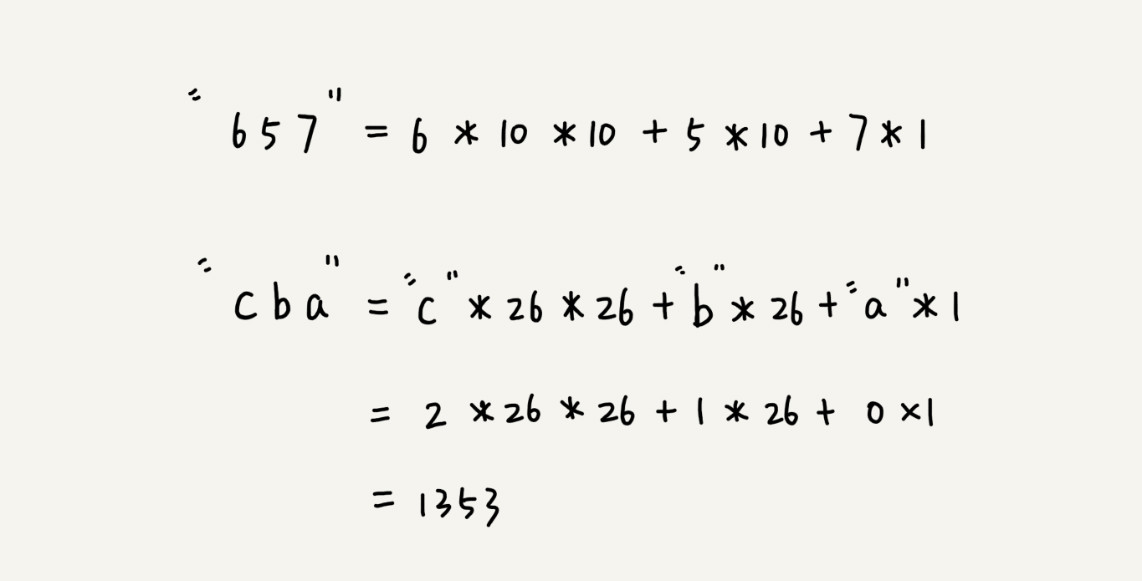
这种哈希算法有一个特点, 在主串中,相邻两个子串的哈希值的计算公式有一定关系。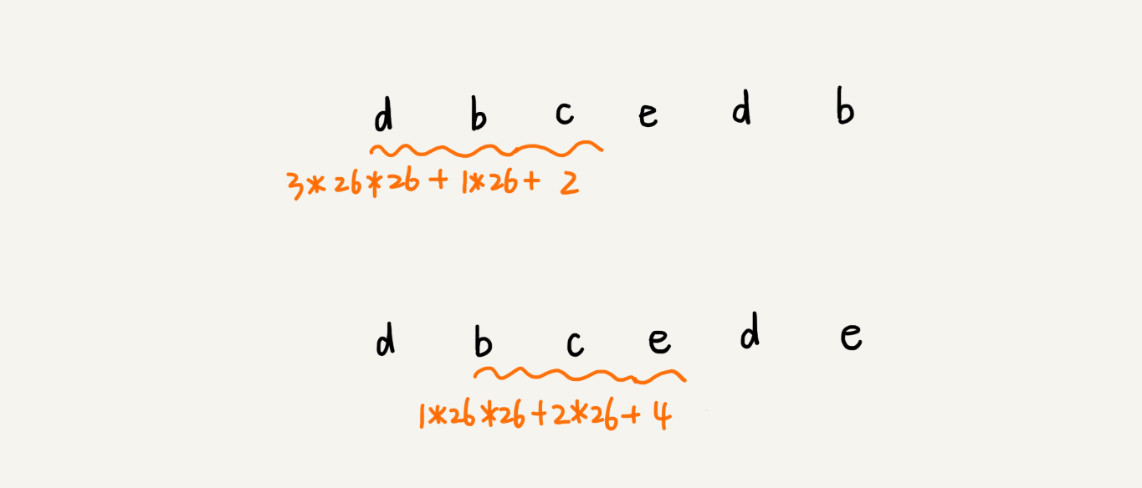
规律:相邻两个子串s[i-1]和s[i] (i 表示子串在主串中的起始位置,子串的长度都为m),对应的哈希值计算公式有交集,可以使用s[i-1]的哈希值很快的计算出s[i]的哈希值。用公式表示: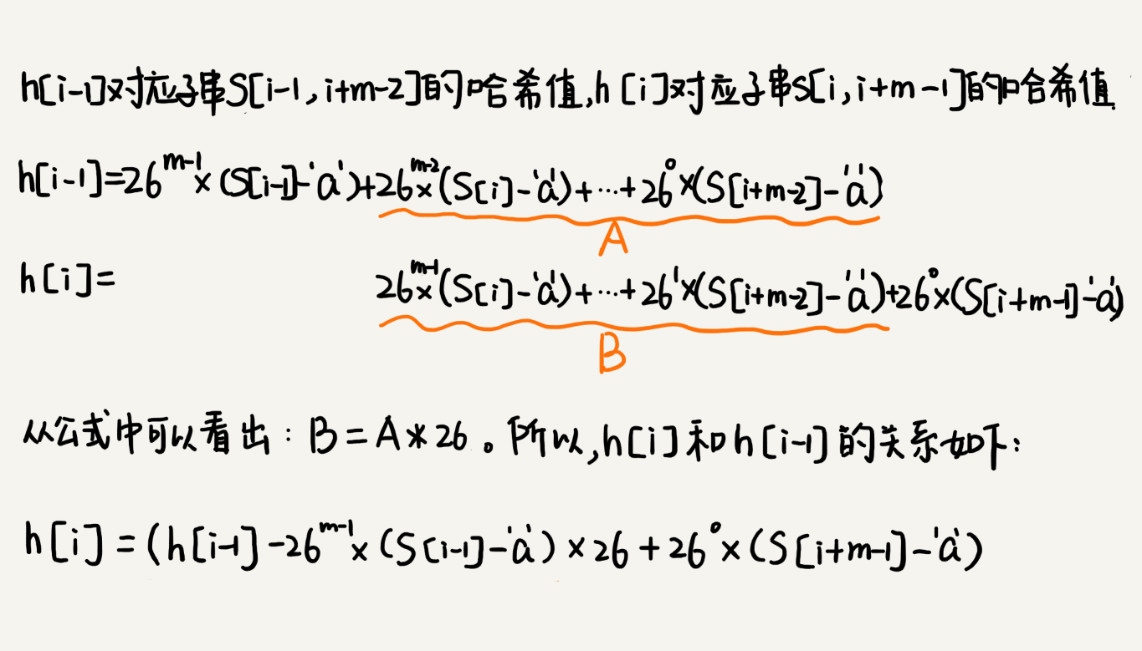
26^(m-1)这部分的计算,我们可以通过查表的方法来提高效率。我们事先计算好26^0、26^1、 2……26^(m -1),并且存储在一个长度为m的数组中,公式中的“次方”就对应数组的下标。当我们需要计算26的x次方的时候,就可以从数组的下标为x的位置取值,直接使用,省去了计算的时间。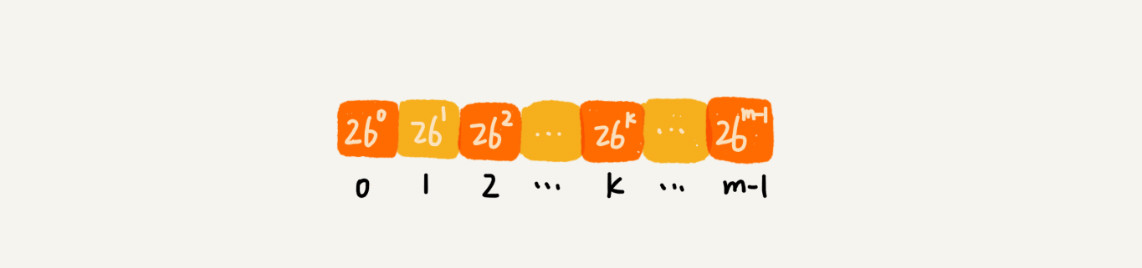
RK算法时间复杂度分析:
整个RK算法包含两部分,计算子串哈希值和模式串哈希值与子串哈希值之间的比较。
第一部分,可以通过设计特殊的哈希算法,只需要扫描一遍主串就能计算出所有子串的哈希值了,这部分的时间复杂度是O(n)。
如果模式串很长,相应的主串中的子串也会很长,通过上面的哈希算法计算得到的哈希值就可能很大,如果超过了计算机中整型数据可以表示的范围,为了能将哈希值落在整型数据范围内,可以牺牲一下, 允许哈希冲突。比如可以将字符串中每个字母对应的数字相加得到哈希值,这样产生的哈希值数据范围就小很多。
当存在哈希冲突的时候,有可能存在这样的情况,子串和模式串的哈希值虽然是相同的,但是两者本身并不匹配。解决方法是当发现一个子串的哈希值跟模式串的哈希值相等的时候,只需要再对比一下子串和模式串本身。
极端情况下,如果存在大量的冲突,每次都要对比字串和模式串本身,时间复杂度会退化为O( n * m)。一般情况下,冲突不会很多,RK算法效率还是比BF算法高。
二维空间
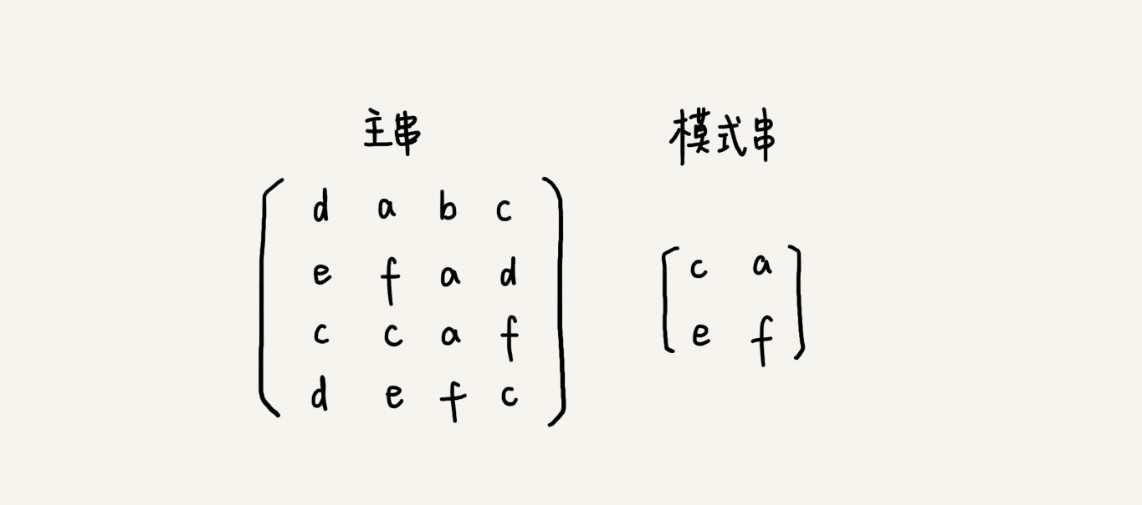
可以同理看做一个字符串来处理。
BM算法
BF,RK算法中遇到不匹配,模式串往后滑动一位,然后从模式串第一个字符开始重新匹配。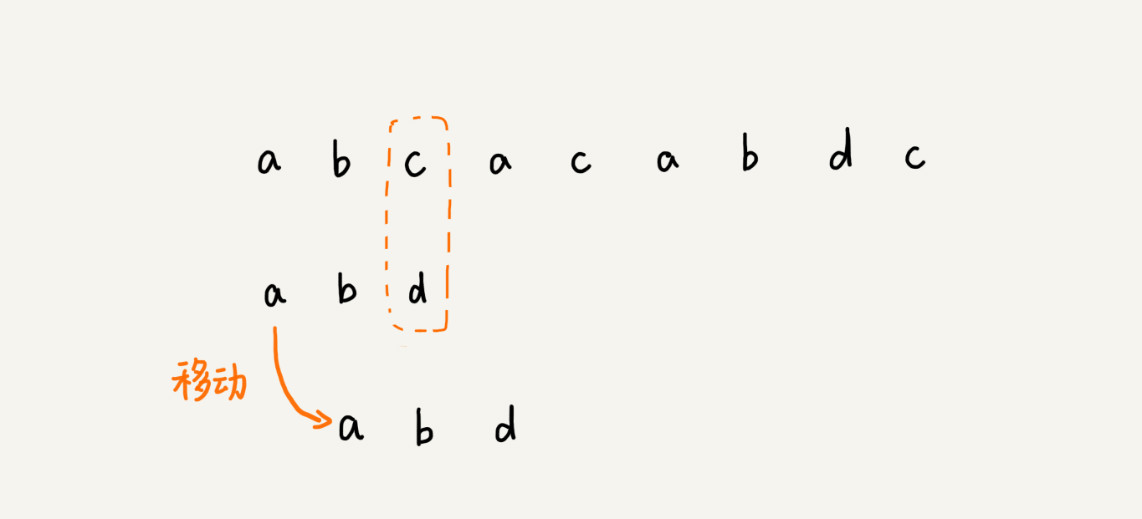
主串中的c,在模式串中是不存在的,模式串向后滑动的时候,只要c与模式串有重合,肯定无法匹配。所以,可以一次性把模式串往后多滑动几位,把模式串移动到c的后面。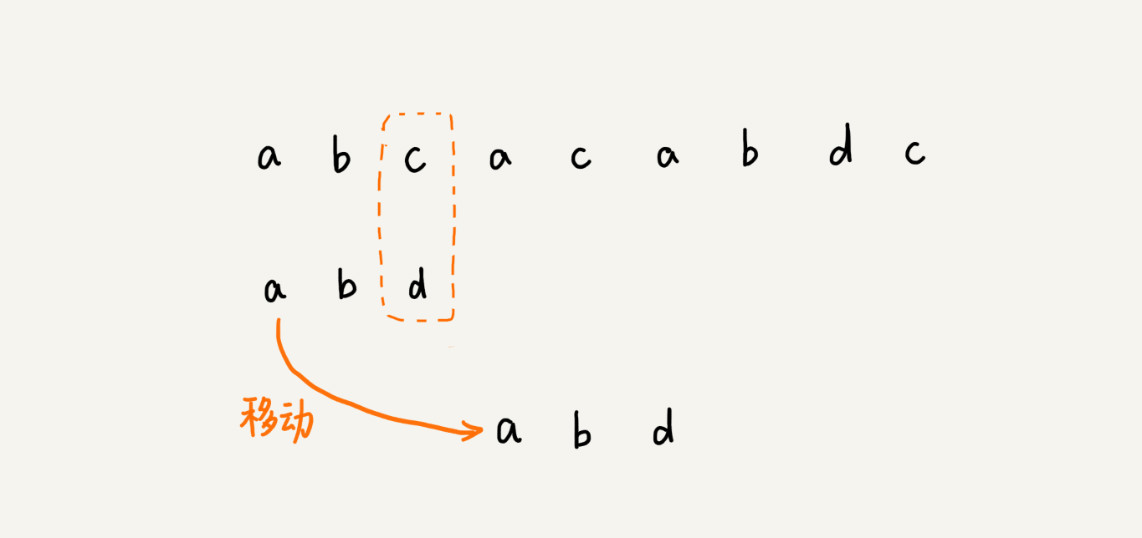
BM算法,本质上其实就是在寻找这种规律。借助这种规律,在模式串与主串匹配的过程中,当模式串和主串某个字符不匹配的时候,能够跳过一些肯定不会匹配的情况,将模式串往后多滑动几位。
BM算法原理分析
BM算法包含两部分,分别是坏字符规则和好后缀规则。
坏字符规则
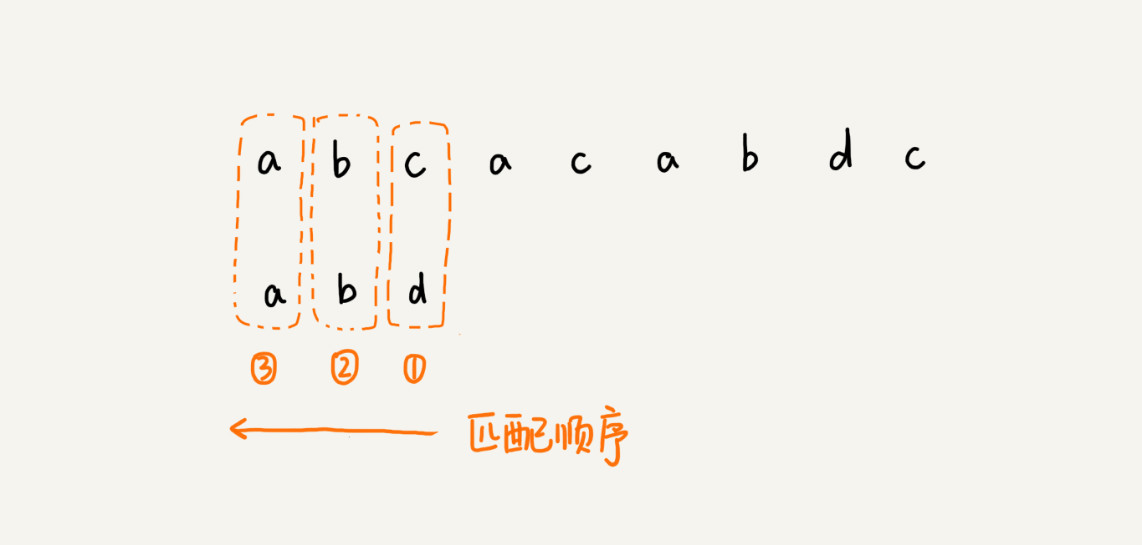
BM算法的匹配顺序比较特别,是按照模式串下标从大到小的顺序,倒着匹配的。当发现某个字符没法匹配的时候。把这个没有匹配的字符叫作坏字符(主串中的字符)。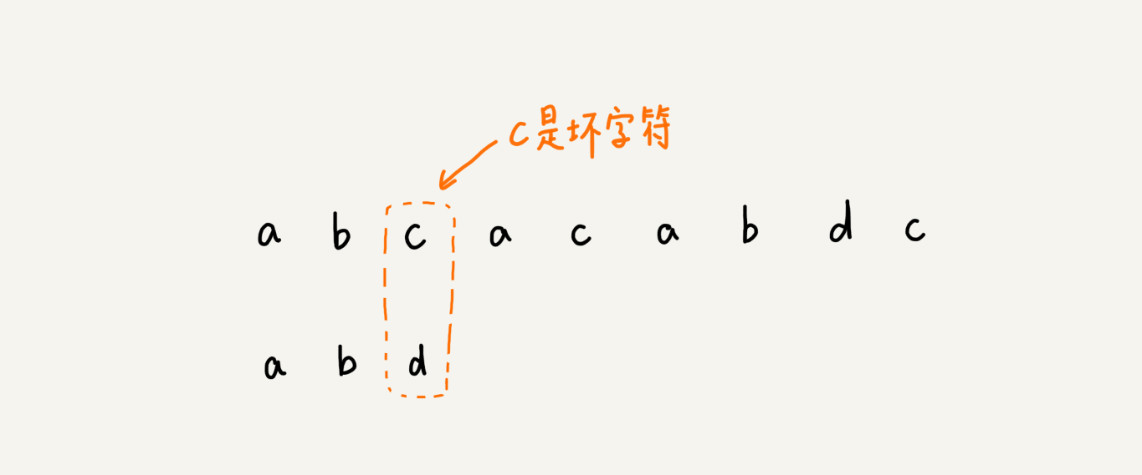
拿坏字符c在模式串中查找,发现模式串中并不存在这个字符,也就是说,字符c与模式串中的任何字符都不可能匹配。这个时候,可以将模式串直接往后滑动三位,将模式串滑动到c后面的位置,再从模式串的末尾字符开始比较。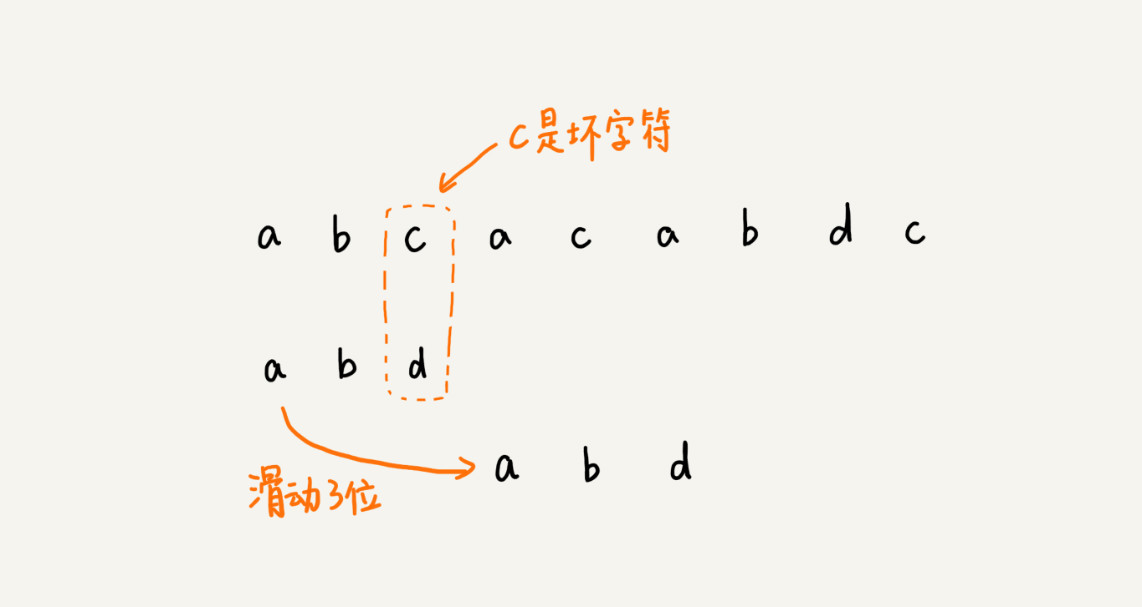
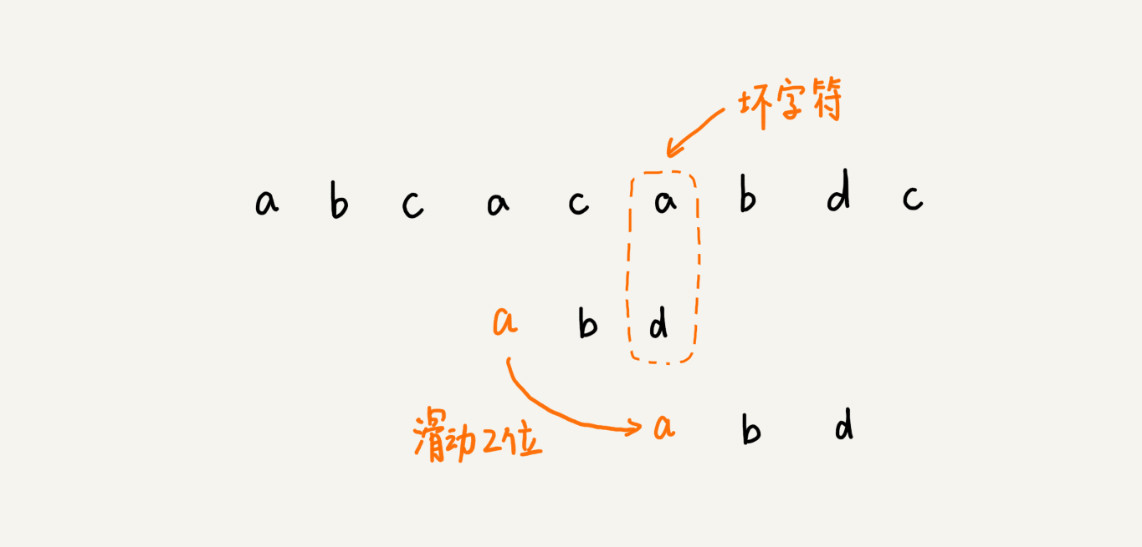
然后对于模式串中存在的a,滑动两位,让两个串对齐。
总结规律为:
当发生不匹配的时候,把坏字符对应的模式串中的字符下标记作si。如果坏字符在模式串中存在,把这个坏字符在模式串中的下标记作xi。如果不存在,把xi记作-1。那模式串往后移动的位数就等于si-xi。(注意, 这里都是字符在模式串的下标)。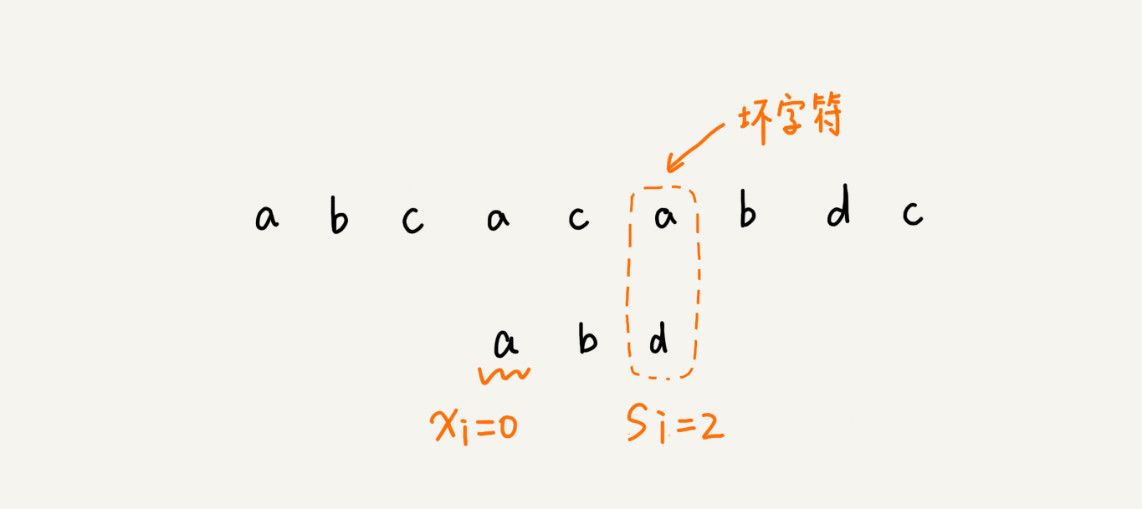
如果坏字符在模式串里多处出现,在计算xi的时候,选择最靠后的那个,这样不会让模式串滑动过多,导致本来可能匹配的情况被滑动略过。
单纯使用坏字符规则还是不够的。因为根据si-xi计算出来的移动位数,有可能是负数。所以,BM算法还需要用到“好后缀规则”
好后缀规则
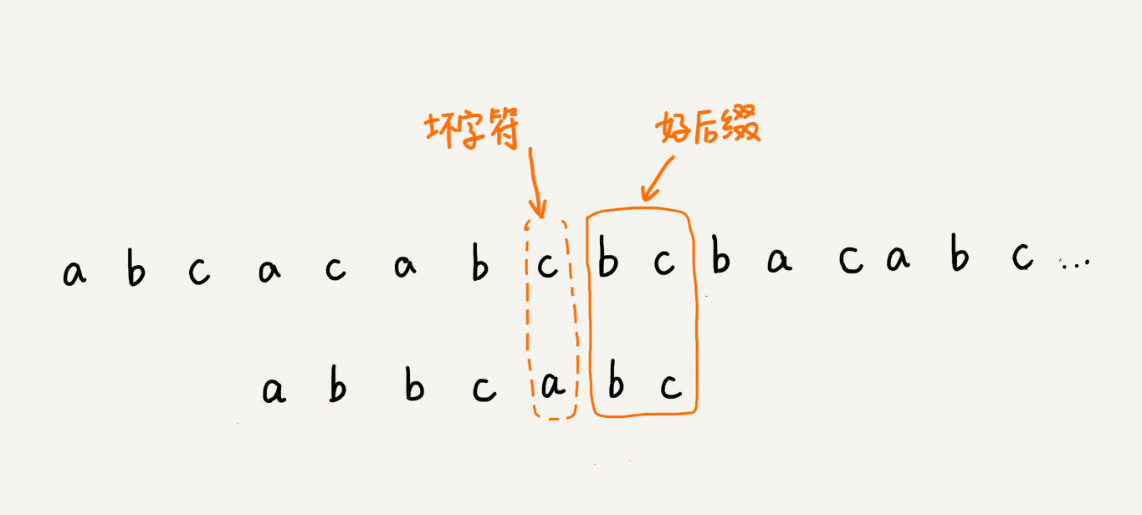
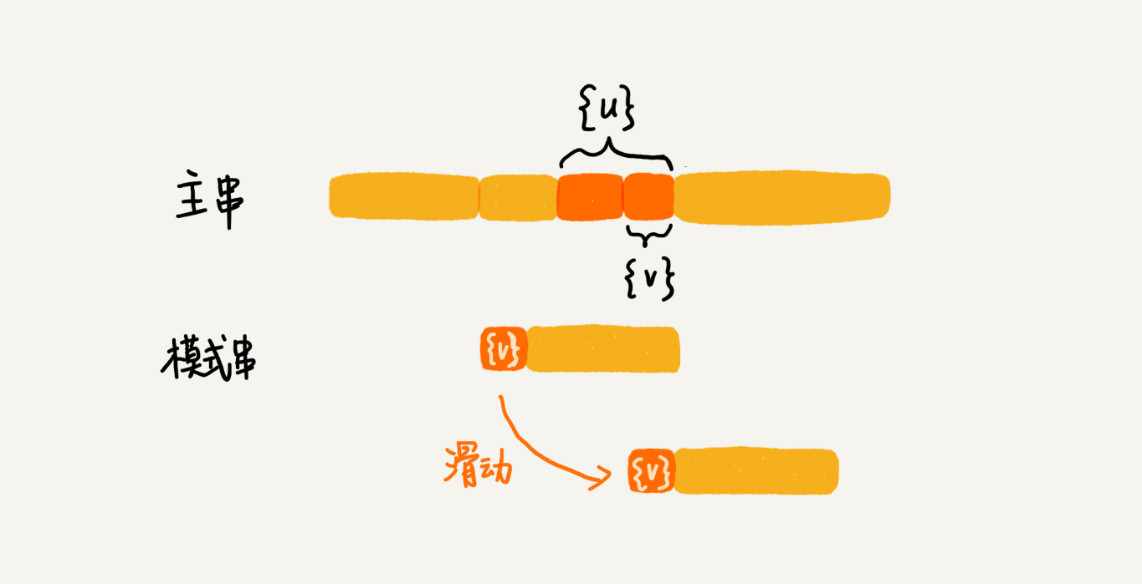
把已经匹配的bc叫作好后缀,记作{u}。我们拿它在模式串中查找,如果找到了另一个跟{u}相匹配的子串{u },那我们就将模式串滑动到子串{u }与主串中{u}对齐的位置。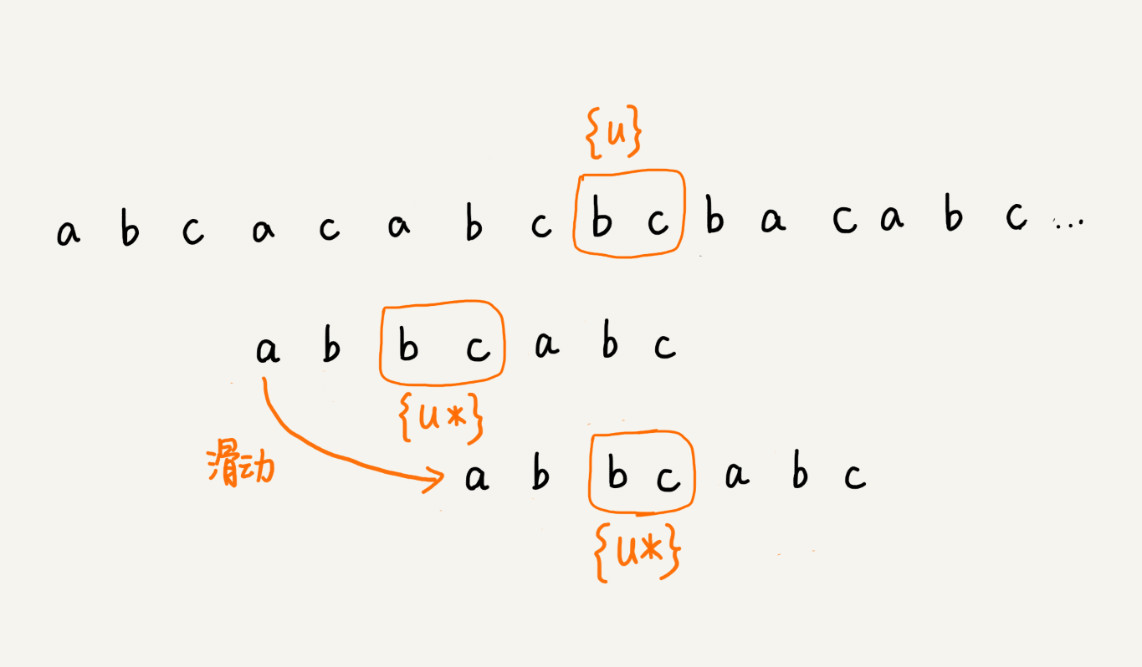
如果在模式串中找不到另一个等于{u}的子串,就直接将模式串滑动到主串中{u}的后面。此时有可能存在滑动过头的情况,错过匹配字符串。所以不仅要看好后缀在模式串中,是否有另一个匹配的子串,还要考察好后缀的后缀子串,是否存在跟模式串的前缀子串匹配的。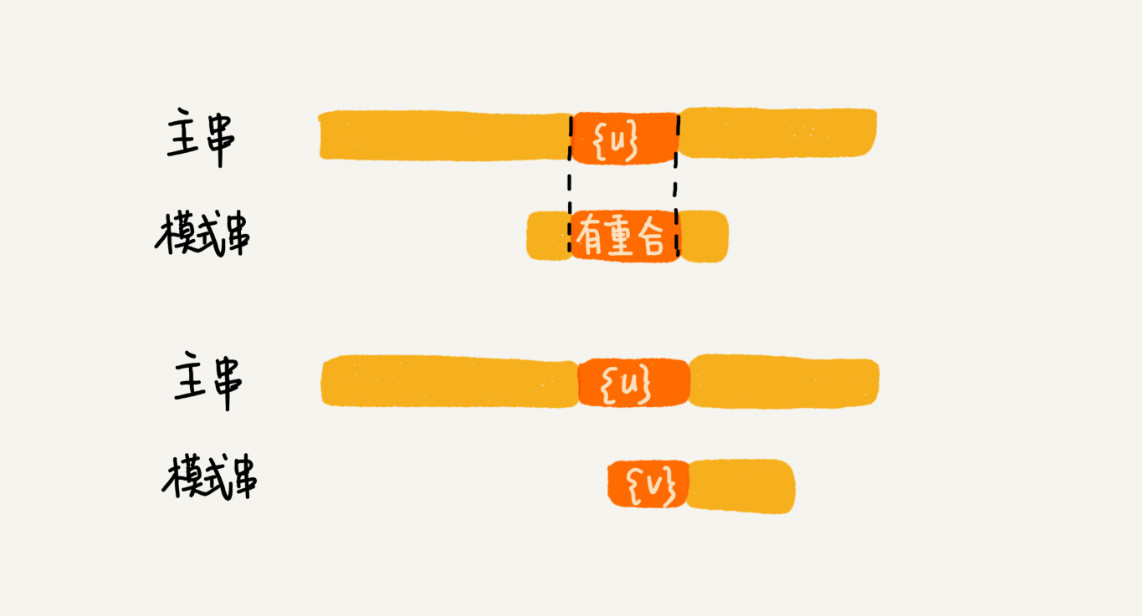
分别计算好后缀和坏字符往后滑动的位数,然后取两个数中最大的,作为模式串往后滑动的位数。这种处理方法还可以避免根据坏字符规则,计算得到的往后滑动的位数,有可能是负数的情况。
BM算法代码实现
坏字符,在模式串中顺序遍历查找,这样就会比较低效,势必影响这个算法的性能。可以将模式串中的每个字符及其下标都存到散列表中。这样就可以快速找到坏字符在模式串的位置下标。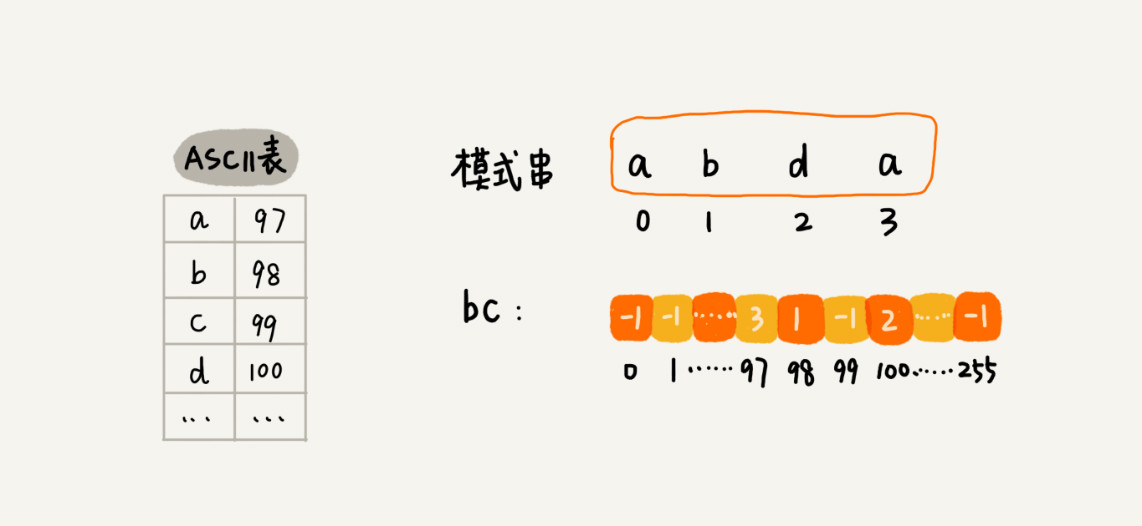
表示模式字串中不同的后缀字串。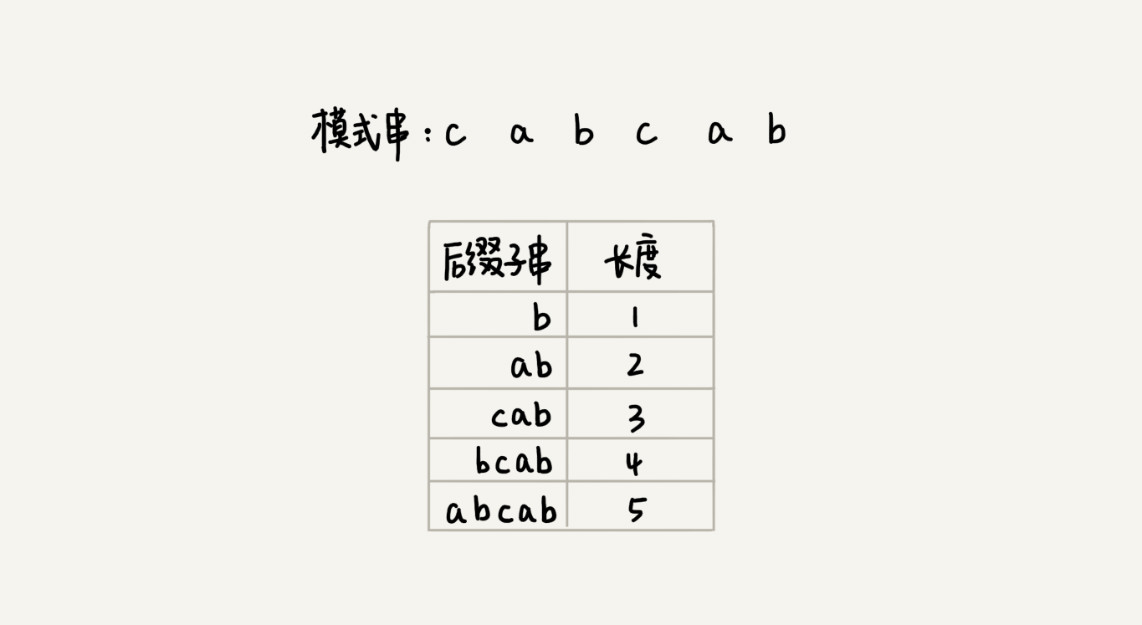
suffix数组下标k,表示后缀字串的长度,下标对应的数组值存储的是在模式串中跟好后缀{u}相匹配的字串{u * }的起始下标值。
不仅要在模式串中,查找跟好后缀匹配的另一个子串,还要在好后缀的后缀子串中,查找最长的能跟模式串前缀子串匹配的后缀子串。
除了suffix数组外,还需要另一个boolean类的prefix数组,来记录模式串的后缀字串能否匹配模式串的前缀字串。
BM算法的性能分析及优化
BM内存消耗,其中bc数组的大小跟字符集大小有关,suffix 数组和prefix数组的大小跟模式串长度m有关。
如果处理字符集很大的字符串匹配问题,bc 数组对内存的消耗就会比较多。因为好后缀和坏字符规则是独立的,如果运行的环境对内存要求苛刻,可以只使用好后缀规则,不使用坏字符规则,这样就可以避免bc数组过多的内存消耗。不过,单纯使用好后缀规则的BM算法效率就会下降一些了。
BM算法核心思想是,利用模式串本身的特点,在模式串中某个字符与主串不能匹配的时候,将模式串往后多滑动几位,以此来减少不必要的字符比较,提高匹配的效率。BM算法构建的规则有两类,坏字符规则和好后缀规则。好后缀规则可以独立于坏字符规则使用。因为坏字符规则的实现比较耗内存,为了节省内存,可以只用好后缀规则来实现BM算法。